Question

At which points tangent line to f(x) = 1/(x^2-25) is horizontal and at which points is it vertical?

Answer 1

we have the function

`f(x)=(1)/(x^2-25)`

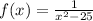
Find out the first derivative of the function f(x)

`f^(\prime)(x)=-(2x)/((x^2-25)^2)`

Part a

At which point the tangent line to f(x) is horizontal

Remember that

If the tangent line is horizontal, then the slope is equal to zero

so

Equate the first derivative to zero

`-(2x)/((x^2-25)^2)=0`

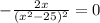
Solve for x

`\begin{gathered} -(2x)/((x^2-25)^2)=0 \\ \\ -2x=0 \\ x=0 \end{gathered}`

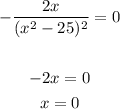
Substitute the value of x=0 in the function f(x)

`f^(\prime)(x)=-(2(0))/((0^2-25)^2)=0`

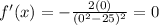
therefore

the point is the origin (0,0)

Part B

At which point the tangent line to f(x) is vertical

Remember that

If the tangent line is vertical, then the slope is undefined

the slope is given by the first derivative

`f^(\prime)(x)=-(2x)/((x^(2)-25)^(2))`

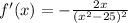
The first derivative is undefined by x=5 and x=-5, but the given function is also undefined at x=5 and at x=-5 (there is a vertical asymptote)

therefore

No points for which the tangent is vertical