Question

What are the equations for the asymptotes of this hyperbola? =1 64 = 55 O Av=1 V5. --VES 5 ty=-V55 5 x, y= 5 V 73 S O B.V=V73 -- = O c. v=zt, y=- OD 1 = 8, y = - 8 Too colon

Answer 1

The Solution:

Given the equation of the hyperbola below:

`(x^2)/(9)-(y^2)/(64)=1`

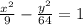
We are required to find the equation for the asymptotes of the above hyperbola.

By formula, the equation for the asymptotes is

`\begin{gathered} y=\pm(b)/(a)x \\ \text{Where} \\ a^2=9 \\ a=\pm3 \\ b^2=64 \\ b=\pm8 \end{gathered}`

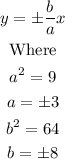
Substituting these values in the formula above, we get

`\begin{gathered} y=\pm(8)/(3)x \\ \text{This becomes} \\ y=+(8)/(3)x\text{ or }y=-_{}(8)/(3)x \end{gathered}`

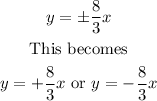
Therefore, the correct answer is option D.