Question

What is the probability of either event occurring when you roll adie?Event A: Rolling a 6Event B: Rolling a number greater than 3Express your answer as a simplified fraction.Enter the answer

Answer 1

Given:

Roll a die.

Required:

We need to find the probability that rolling a 6 and rolling a number greater than 3.

Step-by-step explanation:

A)

A die had six sides and numbered 1 to 6.

The sample space, S=(1,2,3,4,5,6)

`n(S)=6`

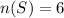
Let event A be rolling a 6.

A={6}.

`n(A)=1`

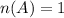
The probability that rolling a 6 is P(A).

`P(A)=(n(A))/(n(S))`
`P(A)=(1)/(6)`

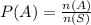
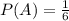
B)

Let B be the event of rolling a number greater than 3.

`B=\lbrace4,5,6\rbrace`
`n(B)=3`

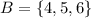
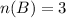
The probability of rolling a number greater than 3 is P(B).

`P(B)=(n(B))/(n(S))`
`P(B)=(3)/(6)`
`P(B)=(1)/(2)`

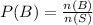
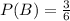
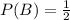
Final answer:

The probability of rolling a 6 is 1/6.

The probability of rolling a number greater than 3 is 1/2.