We know that the empirical rule states that 99.7% of the area is in the interval:
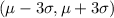
In this case we notice that we are looking at the interval (56,89) in a normal distribution with mean 56 and standard deviation 11, which means that we area in the interval:
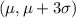
which means that we have half the area of the interval mentioned before. Therefore, the approximate percentage between 56 and 89 is 49.85%