ANSWER:
The vertices of the hyperbola are at (-9, 5) and (1, 5).
Step-by-step explanation:
The vertices of a hyperbola are always aligned in the center of the hyperbola.
Based on the equation, we can easily see that the center of the hyperbola is at (-4, 5). We got the center by equating the numerator into zero and solving x and y.
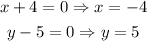
Between the x and y variables in the equation of the hyperbola, the x-variable is positive. Hence, we have a horizontal hyperbola.
Since it is a horizontal hyperbola, the distance between the two vertices and the center is √25 or just 5 units horizontally. We will add and subtract 5 on the coordinates of the center.
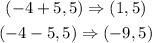
Hence, the vertices of the hyperbola are located at (-9 5) and (1, 5).