Question

The IQ of 10 randomly selected senior high school students are given below. 10212512012811610812411510999Compute the sample mean, variance and standard deviation.

Answer 1

Given:

The IQ of 10 randomly selected senior high school students are given as:

102,125,120,128,116,108,124,115,109,99.

Required:

To compute the sample mean, variance and standard deviation. ​

Step-by-step explanation:

First, we will calculate the sample mean .

Here, the IQ of 10 students is given.

Therefore, total number of students (n) = 10.

Thus,

`\begin{gathered} \bar{x}=(102+125+120+128+116+108+124+115+109+99)/(10) \\ \bar{x}=(1146)/(10) \\ \bar{x}=114.6 \end{gathered}`

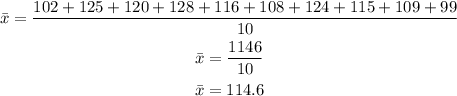
Next, the variance is given as follows:

`S^2=\frac{\sum_{i\mathop{=}1}^n(x_i-\bar{x})^2}{n-1}`

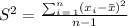
Now, we have,

`\begin{gathered} x_1-\bar{x}=102-114.6=-12.6 \\ x_2-\bar{x}=125-114.6=10.4 \\ x_3-\bar{x}=120-114.6=5.4 \\ x_4-\bar{x}=128-114.6=13.4 \\ x_5-\bar{x}=116-114.6=1.4 \\ x_6-\bar{x}=108-114.6=-6.6 \\ x_7-\bar{x}=124-114.6=9.4 \\ x_8-\bar{x}=115-114.6=0.4 \\ x_9-\bar{x}=109-114.6=-5.6 \\ x_(10)-\bar{x}=99-114.6=-15.6 \end{gathered}`

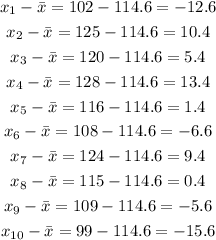
Thus,

`\begin{gathered} S^2=(158.76+108.16+29.16+179.56+1.96+43.56+88.36+0.16+31.36+243.36)/(9) \\ S^2=(884.4)/(9) \\ S^2=98.27 \end{gathered}`

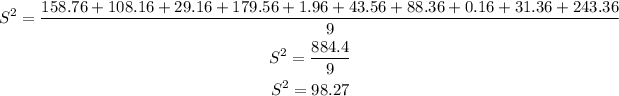
Next, the standard deviation is,

`\begin{gathered} S=√(98.27) \\ S=9.9131 \end{gathered}`

Final Answer:

The mean is 114.6.

The variance is 98.27.

The standard deviation is 9.9131.