The answer is D. None of these are true
Let's analyse item by item.
A) If x→-∞,
the term x² is very large and positive. (-bx) is very large and positive, 3/x → 0
Then y→+∞ and A) is false.
B) Let's plug x=2 in the function:
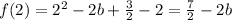
b is a constant, so the value of f(2) is a unique number, this discard the asymptote. => B) is false
C) A y intercept occurs when x=0
f(0)=0²-0b+3/0-2
We have a division by zero, that's an indertermination, and thus C) is false
E) Let's replace y=0 in the equation:
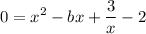
Doing some algebra, we isolate the terms with x on one side. Then rewrite the term with x as a fraction:
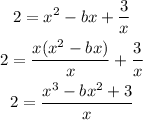
Now we can multiply both sides by x
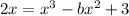
Then,
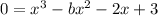
This describes the roots of a cubic equation, and we know that a cubic equation doens't have an asymptote in their roots.
Also you can plot the equation to see that doesn't have an asymptote.
We have discarded all the option except D) that is none is true, then the answer is D)