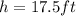Question

Standing 20 feet from a streetlight, a 5-foot tall woman casts an 8-foot shadow. How tall is the streetlight

Answer 1

The height h of the streetlight is 17.5ft

`h=17.5ft`

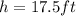
Step-by-step explanation:

The question can be illustrated in the drawing below;

Firstly, we need to find angle x;

`\begin{gathered} \tan x=(5)/(8) \\ x=\tan ^(-1)((5)/(8)) \\ x=32^0 \end{gathered}`

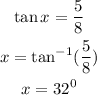
From angle x we can now determine the value of height h of the streetlight;

`\begin{gathered} \tan x=(h)/(28) \\ \tan 32=(h)/(28) \\ h=28*\tan 32 \\ h=28*0.625 \\ h=17.5ft \end{gathered}`

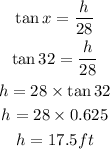
The height h of the streetlight is 17.5ft

`h=17.5ft`