Question

Consider a square and a regular octagon (an 8-sided figure with sides of equal length), One side of thesquare is 7 feet longer than a side of the octagon, and the two figures have the same perimeter. What arethe lengths of the sides of each figure? (Round to two decimal places if necessary.)

Answer 1

Step-by-step explanation:

We are given the following details:

A square and a regular octagon have the same perimeter. However the sides are not given. Let us assign a variable to the sides of the octagon. One side of the octagon would be represented by letter x.

Note that it is a regular octagon which means all eight sides have the same length. Next we are told that one side of the square is 7 feet longer than one side of the octagon. This means one side of the square would be 7 + x. Note that a square too has all four sides with equal length.

Therefore we would hav e the following;

`\begin{gathered} Octagon=x \\ Square=7+x \end{gathered}`

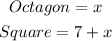
Next we are told the two figures have the same perimeter.

The perimeter of an octagon is;

`\begin{gathered} Octagon: \\ Perimeter=8x \\ Where: \\ x=length\text{ of one side} \end{gathered}`

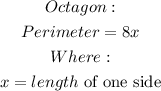
For a square we have;

`\begin{gathered} Square: \\ Perimeter=4x \\ Where: \\ x=length\text{ of one side} \end{gathered}`

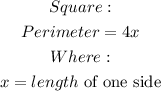
Note however that the length of the square in this instance is (7 + x), hence we can re-write this equation as;

`\begin{gathered} Square: \\ Perimeter=4\left(7+x\right) \end{gathered}`

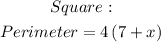
Since the perimeters for both are equal, we can equate both equations and we'll have;

`8x=4\left(7+x\right)`

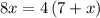
We can now solve for the variable x;

`8x=4\left(7+x\right)`
`8x=28+4x`

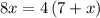
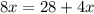
Combine like terms;

`8x-4x=28`
`4x=28`

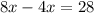
Divide both sides by 4;

`\begin{gathered} (4x)/(4)=(28)/(4) \\ x=7 \end{gathered}`

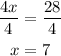
This means the length of a side of the octagon is 7 feet, while the length of a side of the square is 14 feet (7 + 7).

ANSWER:

`\begin{gathered} Octagon=7ft \\ Square=14ft \end{gathered}`