1 Answer

Caleb Brinkman · Answer 1 · 2023-12-31T16:42:21+0000

Solution:

The matrix is given below as

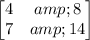
$\begin{bmatrix}{4} & {8} \\ {7} & {14}\end{bmatrix}$

Calculate the determinant of the matrix below

The determinant of the matrix is

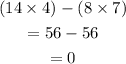
$\begin{gathered} (14*4)-(8*7) \\ =56-56 \\ =0 \end{gathered}$

The inverse of a matrix is calculated using the formula below

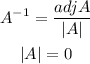
$\begin{gathered} A^(-1)=(adjA)/(|A|) \\ |A|=0 \end{gathered}$

Hence,

The final answer is

NO,THE DETERMINANT IS ZERO

OPTION D is the right answer

Please log in or register to add a comment.