Answer:
The mean deviation for the set of data = 2
Step-by-step explanation:
The given set of data is:
27, 30, 23, 25, 25.
The mean deviation formula for ungrouped data is:
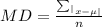
The sample size, n = 5
The mean, µ = (27 + 30 + 23 + 25 + 25)/5
µ = 130/5
µ = 26
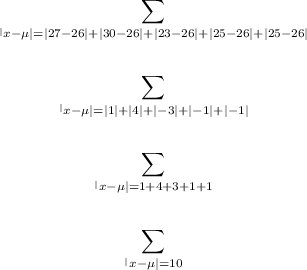
The mean deviation is therefore:
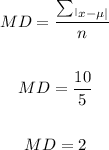
The mean deviation for the set of data = 2