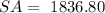Question

"The surface area of a sphere is 205 in^2. If its radius is tripled, what will be the new surface area of the sphere? " If you could help explain how to solve this that would be great! Thank you!

Answer 1

Question:

The surface area of a sphere is 205 in^2. If its radius is tripled, what will be the new surface area of the sphere?

Solution:

The surface area of a sphere is given by the following formula:

`SA=4\pi r^2`

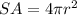
where r is the radius of the sphere. Now, if the surface area of the sphere is 205 in^2, by the above equation we have that:

`205=4\pi r^2`

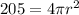
solving for r^2, we get:

`r^2\text{ = }(205)/(4\pi)`

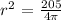
and solving for r, we get:

`r\text{ = }\sqrt[]{(205)/(4\pi)}\text{ = 4.03}`

this means that the radius of the sphere with a surface area of 205 in^2 is 4.03. Then, if this radius is tripled, we get a new radius of

r = 3 x 4.03 = 12.09

then, replacing this new value in the first equation (surface area), we get:

`SA=4\pi(12.09)^2\text{ = 1836.80}`

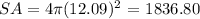
Then, we can conclude that the correct answer is:

`SA=\text{ 1836.80}`