Based on the piecewise function, we have two conditions: if x is equal to 5 and not equal to 5.
Since the given value of x in the question is 3, let's use the first condition that states x is not equal to 5.
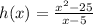
Let's plug in x = 3 in the function above.
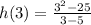
Then, simplify.
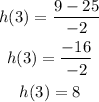
Therefore, h(3) = 8.
Similary, for B, since the given value of x is 0, which is not equal to 5 still, let's use the first condition and plug in x = 0.
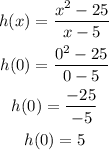
Hence, h(0) = 5.
Lastly, for C, the given value of x is 5. With that, we shall use the second condition.
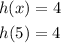
Therefore, h(5) = 4.