we are asked to determine the surface area of the figure. To do that we need to find the areas of each face and add them together. The front face is a trapezoid, and its area is:

Where "b" is the upper base, "B" is the lower base and "h" is the height. Replacing the values:
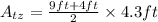
Solving the operations:
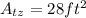
the upper face is a rectangle, its area is the product of its side:
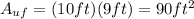
The area of the lower face is also a rectangle, therefore its area is:

The side face is also a rectangle, and its area is:
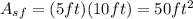
Now we add the areas having into account that the front and side faces repeat themselves. the total surface area is:

replacing the values:
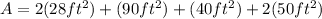
Solving the operations:
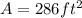
Therefore, the surface area is 286 square feet.