The general slope - intercept form of the line is ;

where m is the slope, b is y-intercept
We need to find the equation of the line containing the points ( -2 , 7 ) and ( 4 , -2 )
The slope will be calculated as following:
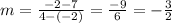
So, the equation of the line will be :
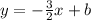
using the point ( -2 , 7 ) to find b:
So, when x = -2 , y = 7
so,
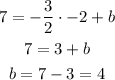
so, the equation of the line is:
