Question

May u please help me with Ap calculsFind the derivate:

Answer 1

`y=\ln (x^2+3)`

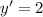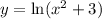
To find the derivate of a equation with natural logarithm you use the next:

`\begin{gathered} y=\ln u \\ y^(\prime)=u^(\prime)(1)/(x) \end{gathered}`

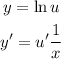
You need to turn the given equation as follow:

`\begin{gathered} y=\ln (x^2+3) \\ y=\ln u \\ u=x^2+3 \end{gathered}`

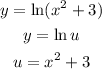
Find the derivate of u:

`\begin{gathered} y=x^n \\ y^(\prime)=nx^(n-1) \end{gathered}`

`\begin{gathered} u^(\prime)=2x+0 \\ u`=2x \end{gathered}`

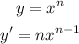
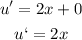
Then, you find the derivate of the natural logarithm:

`\begin{gathered} y=\ln (x^2+3) \\ y^(\prime)=u^(\prime)\cdot(1)/(x^2+3) \\ \\ y^(\prime)=(2x)/(x^2+3) \end{gathered}`

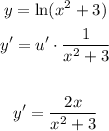
The answer is:

`y^(\prime)=(2x)/(x^2+3)`

-------------------------------------------------

`y=2x\sin x`

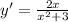
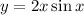
You use the next formula for the derivate of a product:

`\begin{gathered} y=xg \\ y^(\prime)=xg^(\prime)+gx^(\prime) \end{gathered}`
`\begin{gathered} y=\sin x \\ y^(\prime)=\cos x \end{gathered}`

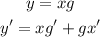
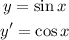
You get:

`\begin{gathered} y^(\prime)=2x\cos x+\sin x(2x^0) \\ y^(\prime)=2x\cos x+2\sin x \end{gathered}`

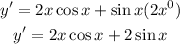
In x=π/2

`\begin{gathered} y^(\prime)=2((\pi)/(2))\cos ((\pi)/(2))+2\sin ((\pi)/(2)) \\ \\ y^(\prime)=\pi\cos (\pi)/(2)+2\sin (\pi)/(2) \\ y^(\prime)=\pi(0)+2(1) \\ \\ y^(\prime)=2 \end{gathered}`

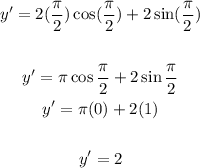
The answer is

`y^(\prime)=2`