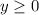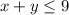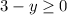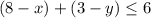Question

A foreign-car dealer with warehouses in New York and Baltimore receives orders from dealers in Philadelphia and Trenton. The dealer would to minimize the shipping cost. The dealer in Philadelphia needs 3 cars and the dealer in Trenton needs 8. The New York warehouse has 5 cars and the Baltimore warehouse has 9. The cost of shipping cars from Baltimore to Philadelphia is $120 per car, from Baltimore to Trenton $90 per car, from New York to Philadelphia $100 per car, and from New York to Trenton $70 per car. Let x be the number of cars shipped from Baltimore to Trenton, and y be the number of cars shipped from Baltimore to Philadelphia. 5. Write the six inequalities associated with this problem.

Answer 1

`x \ge 0`

`y \ge 0`

`x + y \le 9`

`8 - x \ge 0`

`3 - y \ge 0`

`(8 - x) + (3 - y) \le 6`

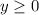
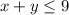
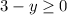
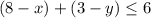
Explanation:

Given

x = Cars from Baltimore to Trenton

y = Cars from Baltimore to Philadelphia

Required

Write out 6 inequalities

First, 0 or more cars must be shipped to both locations

So:

`x \ge 0`

`y \ge 0`

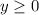
Considering the warehouse in Baltimore.

(1) The warehouse can not ship more than the number of car it has (9).

So:

`x + y \le 9`

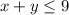
Considering the warehouse in New York.

(1) After shipping cars to Trenton and Philadelphia, the warehouse will have 0 or more cars.

So:

`8 - x \ge 0` --- To Trenton

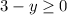`3 - y \ge 0` --- To Philadelphia

(2) The warehouse cannot send out more than 6.

So:

`(8 - x) + (3 - y) \le 6`

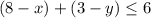
So, the inequalities are:

`x \ge 0`

`y \ge 0`

`x + y \le 9`

`8 - x \ge 0`

`3 - y \ge 0`

`(8 - x) + (3 - y) \le 6`