Given the roots of a quadratic equation as 5 and 6 with a leading coefficient of 3
To get the quadratic equation, we would find the two factors of the quadratic equation and multiply the factors with the leading coefficient as shown below:
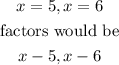
The quadratic equation would be
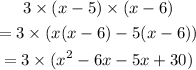
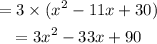
Hence, the quadratic equation is 3x²-33x+90