We are to compare the cost of each rose sold by two florists.
Mom's florist sells ( n ) number of roses at a certain price ( S ) as follows:
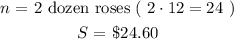
First florist sells ( k ) number of roses at a certain price ( M ) as follows:
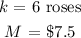
We will determine the cost price of each rose ( c ) sold by the two florist.
For Mom's florist:
We will take the ratio of the total cost ( S ) and the number of roses sold ( n ) as follows:
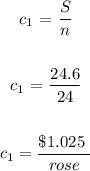
For First florist:
We will take the ratio of the total cost ( M ) and the number of roses sold ( k ) as follows:
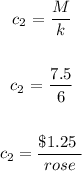
Then we compare the cost prices ( c ) for roses sold by each florist:
![\begin{gathered} c_1Hence,[tex]\text{Mom's florist has the lower cost per rose}]()