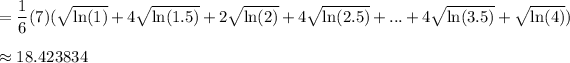Question

Calculus 2

Use the Trapezoidal Rule, the Midpoint Rule, and Simpson's Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.)

`\int\limits^4_1 7√(ln(x)) \, dx` , n=6

Answer 1

See Below.

Explanation:

We want to estimate the definite integral:

`\displaystyle \int_1^47√(\ln(x))\, dx`

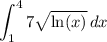
Using the Trapezoidal Rule, Midpoint Rule, and Simpson's Rule with six equal subdivisions.

1)

The trapezoidal rule is given by:

`\displaystyle \int_(a)^bf(x)\, dx\approx(\Delta x)/(2)\Big(f(x_0)+2f(x_1)+...+2f(x_(n-1))+f(x_n)\Big)`

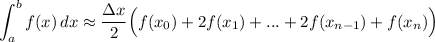
Our limits of integration are from x = 1 to x = 4. With six equal subdivisions, each subdivision will measure:

`\displaystyle \Delta x=(4-1)/(6)=(1)/(2)`

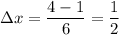
Therefore, the trapezoidal approximation is:

`\displaystyle =(1/2)/(2)\Big(f(1)+2f(1.5)+2f(2)+2f(2.5)+2f(3)+2f(3.5)+2f(4)\Big)`

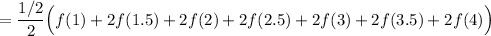
Evaluate:

`\displaystyle =(1)/(4)(7)(√(\ln(1))+2√(\ln(1.5))+...+2√(\ln(3.5))+√(\ln(4)))\\\\\approx18.139337`

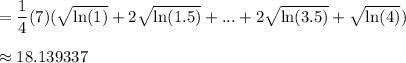
2)

The midpoint rule is given by:

`\displaystyle \int_a^bf(x)\, dx\approx\sum_(i=1)^nf\Big((x_(i-1)+x_i)/(2)\Big)\Delta x`

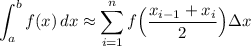
Thus:

`\displaystyle =(1)/(2)\Big(f\Big((1+1.5)/(2)\Big)+f\Big((1.5+2)/(2)\Big)+...+f\Big((3+3.5)/(2)\Big)+f\Big((3.5+4)/(2)\Big)\Big)`

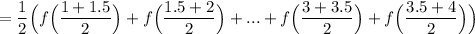
Simplify:

`\displaystyle =(1)/(2)(7)\Big(f(1.25)+f(1.75)+...+f(3.25)+f(3.75)\Big)\\\\ =(1)/(2)(7) (√(\ln(1.25))+√(\ln(1.75))+...+√(\ln(3.25))+√(\ln(3.75)))\\\\\approx 18.767319`

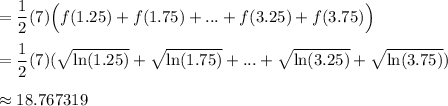
3)

Simpson's Rule is given by:

`\displaystyle \int_a^b f(x)\, dx\approx(\Delta x)/(3)\Big(f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+...+4f(x_(n-1))+f(x_n)\Big)`

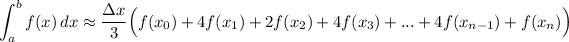
So:

`\displaystyle =(1/2)/(3)\Big((f(1)+4f(1.5)+2f(2)+4f(2.5)+...+4f(3.5)+f(4)\Big)`

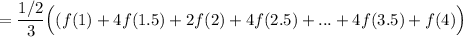
Simplify:

`\displaystyle =(1)/(6)(7)(√(\ln(1))+4√(\ln(1.5))+2√(\ln(2))+4√(\ln(2.5))+...+4√(\ln(3.5))+√(\ln(4)))\\\\\approx 18.423834`