Answer: C. WX/RS = 3/6
Step-by-step explanation:
In the triangle WXY the vertical side is WX, and the horizontal side is XY.
In the triangle RST the vertical side is RS, and the horizontal side is ST.
Since both triangles are similar, this means that their angles have the same measurements, and that there is a propotion or relationship between their sides.
The corresponding sides in this triangle are the following:
WX is a corresponding side with RS
XY is a corresponding side with ST
WY is a corresponding side with RT
Out of the options that we have, the only one that relates two corresponding sides is:
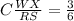
This is because as we pointed out, WX ans RS are correponding sides.
Also from the image we see that WX = 3 and RS = 6 wich is correctly placed in option C. Thus C represents the proportion between the two corresponding sides.
Answer: C. WX/RS = 3/6