Answer:
There is not convincing evidence at the a = 0.05 significance level that the true mean service time during the early morning shift is less than 4 minutes
Explanation:
The null hypothesis is:
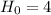
The alternate hypothesis is:

The test statistic is:
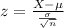
In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
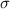 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
From a random sample of 41 orders, the mean time was 3.75 minutes with a standard deviation of 1.2 minutes.
This means that
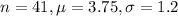
The test-statistic is:
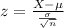
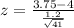

 has a pvalue of 0.0918, looking at the z-table.
has a pvalue of 0.0918, looking at the z-table.
0.0918 > 0.05, which means that the null hypothesis is accepted, and that there is not convincing evidence at the a = 0.05 significance level that the true mean service time during the early morning shift is less than 4 minutes