Question

26) The patient is to receive an intravenous injection of medication. In order to work properly, the pressure of fluid containing the medication must be 109 kPa at the injection point. (a) If the fluid has a density of 1020 kg/m3, find the height at which the bag of fluid must be suspended above the patient. Assume that the pressure inside the bag is one atmosphere. (b) If a less dense fluid is used instead, must the height of suspension be increased or decreased? Explain.

Answer 1

Given,

The pressure of the medication at the injection point, P₁=109 kPa

The density of the fluid, ρ=1020 kg/m³

The pressure inside the bag, P₂=1 atm=101.33 kPa

The difference in the pressure of the fluid is given by the formula,

`\Delta P=P_1-P_2=\rho gh`

Where g is the acceleration due to gravity and h is the height at which the bag of fluid must be suspended.

(a) On substituting the known values in the above equation,

`\begin{gathered} 109*10^3-101.33*10^3=1020*9.8* h \\ \Rightarrow h=(7.67*10^3)/(9996) \\ =0.77\text{ m} \end{gathered}`

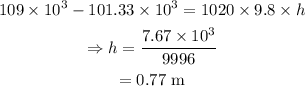
Thus the bag of the fluid must be suspended at a height of 0.77 m.

(b)

On rearranging the above equation,

`\rho=(\Delta P)/(gh)`

Thus the density of the fluid is inversely proportional to the height of suspension of the bag. Thus if the density of the fluid is decreased, i.e., a less dense fluid is used, the height of suspension must be increased.