Question

Use the above (rounded) slope and y-value to write the equation of the tangent line to the graph of f(x)at x=3. Write your answer in mx+b format.

Answer 1

In order to calculate the slope of f(x) at x = 3, we can use the formula below:

`m=(f(x+h)-f(x))/(h)`

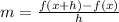
For x = 3 and h = 0.001, we have:

`\begin{gathered} m=(f(3.001)-f(3))/(0.001) \\ f(3.001)=4.8\cdot3.001^2-4.6\cdot3.001=43.2288048-13.8046=29.4242048 \\ f(3)=4.8\cdot3^2-4.6\cdot3=43.2-13.8=29.4 \\ m=(29.4242048-29.4)/(0.001)=(0.0242048)/(0.001)=24.2 \end{gathered}`

The value of f(3), as calculated above, is 29.4.

The tangent line has a slope of m = 24.2 and it passes through the point (3, 29.4), so let's calculate the value of b:

`\begin{gathered} y=mx+b \\ 29.4=24.2\cdot3+b \\ 29.4=72.6+b \\ b=29.4-72.6 \\ b=-43.2 \end{gathered}`

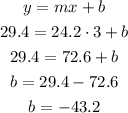
Therefore the equation of the tangent line is y = 24.2x - 43.2.