Question

In 2000, the profit of Company A was $9,875,000. Each year after 2000, the profits fell by $29,532 on average. Construct a linear model for this scenario and use it to solve for profits in the year 2030.

Answer 1

Given:

In 2000, the profit of Company A was $9,875,000.

Each year after 2000, the profits fell by $29,532 on average.

So, the losses of the profit per year = $29,532

We will construct a linear model for this scenario

Let the number of years after 2000 = x

And the profit after the year 2000 = y

the linear model will be: y = mx + b

Where m is the slope which represents the losses per year and the b is the initial profit of the year 2000

So, the linear model will be:

`y=-29,532x+9,875,000`

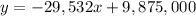
now, we will use the equation to find the profit in the year 2030

so, x = 2030 - 2000 = 30

substitute x = 30 into the equation:

`y=-29,532(30)+9,875,000=8,989,040`

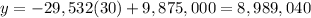
So, the answer will be:

The equation of the model: y = -29532x + 9875000

The profit in the year 2030 = 8989040