Question

In a survey of 29 instructors, it was found that 22 liked white boards, 11 liked blackboards, and 7 liked both. How many instructors did not like white boards?

Answer 1

We need to find the number of instructors that did not like whiteboards.

In order to do so, notice that from the 11 instructors who liked blackboards, 7 also liked whiteboards.

Thus, among the instructors who liked at least one of the two types of boards, the number of them who didn't like whiteboards is:

`11-7=4`

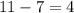
Also, there were some instructors among the whole group of 29 that didn't like any of the two boards. Thus, those ones didn't like whiteboards.

The following image illustrates this problem:

So, we need to find x and add it to the other 4 instructors that didn't like whiteboards.

We have:

`\begin{gathered} 15+7+4+x=29 \\ \\ 26+x=29 \\ \\ x=29-26 \\ \\ x=3 \end{gathered}`

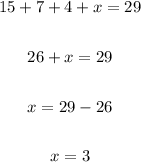
Thus, another 3 instructors didn't like whiteboards.

Therefore, the total number of instructors who didn't like whiteboards is

`4+3=7`

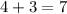
Notice that we can find the same result in a faster way: since 22 instructors liked whiteboards from a total of 29 instructors, it means that 29 - 22 = 7 didn't like whiteboards.

Therefore, the answer is 7.