Given: Michael earns $150 per day washing cars.
x is the number of hours
y is the number of cars
His hourly wage = $10 per hour
He earns $6 for every car.
so, 10x + 6y = 150
So, to find the number of hours and the number of cars, we will make a relation between x and y
Both x and y is greater than 0
As shown, the answer will be the line segment between the points
( 0, 25 ) and ( 15, 0 )
So, one solution is ( 3, 20 )
so, he can work for 3 hours, during it can wash 20 cars
The other possible solutions are:
( 6, 15 ) , ( 9, 10 )
we will write the equation: 10x + 6y = 150
In slope intercept form as follows:

subtract ( 10x ) from both sides:
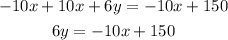
divide both sides by 6
