Question

Select whether the pair of lines is parallel, perpendicular, or neither?how do I solve this?

Answer 1

The pair of lines are perpendicular.

Step-by-step explanation:

The general slope-intercept form of the equation of a straight line is given as;

`y=mx+b`

where m = slope and b = y-intercept.

Given the below equations of a line;

`\begin{gathered} y=-(1)/(2)x-12 \\ y-3=2(x+2) \end{gathered}`

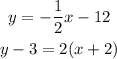
We can see that the 1st equation is in the form of the standard slope-intercept equation but the 2nd equation isn't. So let's go ahead and rewrite the 2nd equation in form of a slope-intercept equation;

`\begin{gathered} y-3=2x+4 \\ y=2x+4+3 \\ \therefore y=2x+7 \end{gathered}`

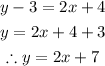
So the two equations are now in the form of a standard slope-intercept equation.

Note that parallel lines have the same slope while the slopes of two perpendicular lines are negative reciprocals of each other.

So if we compare the slopes of the 1st equation and the 2nd equation, we can see that the slope of the 1st equation is the negative reciprocal of the 2nd equation;

`\begin{gathered} m_1=-(1)/(2) \\ m_2=2 \end{gathered}`

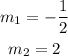
So the pair of lines are perpendicular.