We are given that a car accelerates from 50 m/s to 65m/s in 15 seconds. To determine the force that causes the acceleration we need to determine first the acceleration of the car. To do that we will use the following equation of motion:
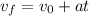
Where:

We solve for the acceleration first by subtracting the initial velocity from both sides:
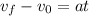
Now we divide both sides by "t":
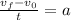
Now we plug in the known values:
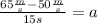
Now we solve the operations, we get:
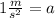
Now, we use Newton's second law to determine the mass. The law states that the force of an object is directly proportional to its mass. This can be written mathematically as:
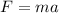
Now we solve for the mass by dividing both sides by the acceleration:
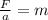
Now we plug in the values:
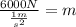
Solving the operations we get:
![6000\operatorname{kg}=m]()
Therefore, the mass of the car is 6000 kilograms.