Given the function f(x):
![f(x)=\sqrt[3]{3x}](https://img.qammunity.org/2023/formulas/mathematics/college/uv7zmj6dqu1l1x9eil9150ntoozxfmxd1o.png)
And the function g(x):
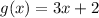
You can find

by dividing the function f(x) by the function g(x).
Then you can set up the following:
![((f)/(g))(x)=\frac{\sqrt[3]{3x}}{3x+2}](https://img.qammunity.org/2023/formulas/mathematics/college/64qyux2dujsw7xqjduogp23lw301qlmdu6.png)
Now, to find the restrictions, you need to remember that the denominator can't be zero. Then, you can set up this equation:
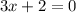
Solve for "x":
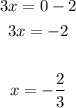
Therefore, you can conclude that:
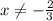
Based on the above, you know that the answer is: Option A.