Question

3.54.03.64.02.62.46.84.94.55.43.72.93.74.73.4Find the mean and sample standard deviation of these data. Round to the nearest hundredth.mean_____sample standard deviation________

Answer 1

The number of terms is 15.

The means is defined as the ratio of sum of terms by number of terms.

Mean:

Determine the mean of the data.

`\begin{gathered} \mu=(3.5+4.0+3.6+4.0+2.6+2.4+6.8+4.9+4.5+5.4+3.7+2.9+3.7+4.7+3.4)/(15) \\ =(60.1)/(15) \\ =4.0066 \\ \approx4.01 \end{gathered}`

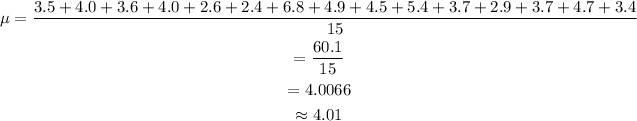
Standard deviation:

Determine the sum of square of difference between each observation and mean of the data.

`\begin{gathered} \sum ^n_(i\mathop=1)(x_i-\mu)^2=(3.5-4.01)^2+(4.0-4.01)^2+(3.6-4.01)^2+(4.0-4.01)^2+(2.6-4.01)^2 \\ +(2.4-4.01)^2+(6.8-4.01)^2+(4.9-4.01)^2+(4.5-4.01)^2+(5.4-4.01)^2 \\ +(3.7-4.01)^2+(2.9-4.01)^2+(3.7-4.01)^2+(4.7-4.01)^2+(3.4-4.01)^2 \end{gathered}`
`\begin{gathered} =0.2601+0.0001+0.1681+0.0001+1.9881+2.5921+7.7841+0.7921+0.2401 \\ +1.9321+0.0961+1.2321+0.0961+0.4761+0.3721 \end{gathered}`
`=18.0295`

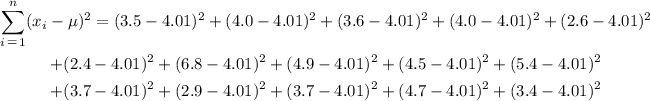
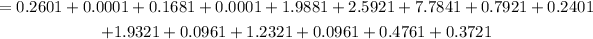
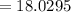
The formula for the statndard deviation is,

`\sigma=\sqrt[]{(\sum ^n_(i\mathop=1)(x_i-\mu)^2)/(n-1)}`

Substitute the values in the formula to determine the standard deviation of the data.

`\begin{gathered} \sigma=\sqrt[]{(18.0295)/(15-1)} \\ =\sqrt[]{(18.0295)/(14)} \\ =1.1348 \\ \approx1.13 \end{gathered}`

Answer:

Mean: 4.01

Standard deviation: 1.13