Answer:
5,697 km
Step-by-step explanation:
The distance along the north-south line (longitude) is a distance along a great circle.
Given City A at 20°N, and City B at 31°S:
Step 1: Find the angular difference:
Note that since they are on a different axis, we add:
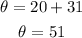
Step 2: Find the distance:
![\begin{gathered} \text{Distance along a great circle}=(\theta)/(360)*2\pi R \\ =(51\degree)/(360\degree)*2*\pi*6400 \\ =5696.8\operatorname{km} \\ \approx5697\operatorname{km} \end{gathered}]()
The distance in kilometers between cities A and B is 5,697km (to the nearest km).