27)
Opposite angles are equal.
x° angle is the opposite angle of the 90° angle.
Therefore, x°=90°.
28)
The 90° angle marked in the figure and the y° angles forms a linear pair.
Hence, both angles are supplementary. Supplementary angles sum upto 180°.
Therefore, we can write

Therefore, y°=90°.
29)
In the figure, let z°+46°=p°.
From figure, we can see that the p° angle is the opposite angle of y° angle.
Since opposite angles are equal, we can write
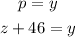
Since from part 28, y°=90°, we get
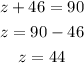
Therefore, zh=44e.
30)
From figure,
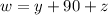
Substitute the known values.
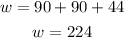
Therefore, w°=224°