Question

The tables below represent two linear equations. Use these table to determine if the lines are parallel, perpendicular or neither. Fill in the blank by choosing the correct response. The linear equations represented by the tables below are [ Select ] [ Select ] TABLE 1 TABLE 2 perpendicular у parallel -2 4 -2 0 neither parallel or perpendicular -1 5 -1 -1 0 6 0 -2 1 7 1 -3 2 8 2. -4

Answer 1

In this case, we'll have to carry out several steps to find the solution.

Step 01:

Data

Table 1

point 1 (0, 6 ) x1 = 0 y1 = 6

point 2 (1 , 7) x2 = 1 y2 = 7

Table 2

point 1 (0 , -2) x1 = 0 y1 = -2

point 2 (1 , -3) x2 = 1 y2 = -3

perpendincular, parallel or neither = ?

Step 02:

Table 1

slope formula

`m1\text{ = }(y2-y1)/(x2-x1)=(7-6)/(1-0)=(1)/(1)=1`

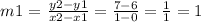
Table 2

slope formula

`m2\text{ = }(-3-(-2))/(1-0)=(-3+2)/(1)=(-1)/(1)=-1`

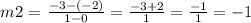
Slope of the perpendicular line, m’

m ' = - 1 / m

m2 = - 1 / m1

-1 = - 1 / 1

-1 = -1

The answer is:

The lines are perpendicular.