Step-by-step explanation
One way to study how well does a function fit a set of data is by looking at the sum of the square differences. Let's assume that (x',y') is a point in the data set and f(x) is a function that fits the data set. Then the square difference for that data point is:
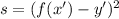
The idea here is to find all the square differences between a function and all the data points and then add them. The function with the smallest sum will be the one that best fits the data.
We can start with the function from option A:
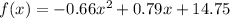
We first need to find the values of f(x) for all the x-values of the data points and then we are going to use these results to find the square differences:

Then we find the square differences using these six values of f(x) and the y-values of the data points:

Then we add these 5 square differences and we obtain:

And this is the number that we must compare.
Then we continue with option B:
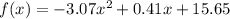
We find the six values of f(x) using the x-values from the data:
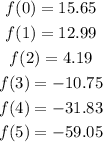
Now the following step would be to find the square differences and then add them. However we don't need to do that, remember that each square difference is a positive number because is given by the square of another value. This means that if we find that one of the square differences is greater than 10.4079 then we can assure that the sum of the square differences of function B is greater than that of the function in A and therefore B is not the best fit and can be discarded.
We can find the square difference related to f(5):
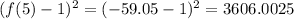
3606.0025 is far greater than 10.4079 so we can discard option B since the function from A is a better fit.
Then we continue with C:
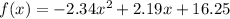
We find the 6 values of f(x) as we did before:
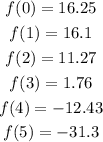
Just like we did in option B we can find the square difference of a value that differs a lot from the one in the data point. We can find the square difference for x=5:
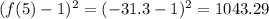
Again this number is far greater than the sum of the square differences from option A so the fit in C is worse than that in A and we can discard this option.
Then we continue with the model in option D:

We find the 6 values of f(x):

Using the same argument as before we can calculate the square difference of a single point. We find that of x=5:
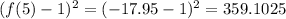
This value is greater than 10.4079 so the function in option A is a better fit than the function in D.
Answer
Then the answer is option A.