Question

In great detail, describe how to solve the advanced function below.4^(8 - 2x) = 256I understand the solution to the problem is (2). I would like a detailed description of how exactly to solve this problem. Having some trouble describing this problem in a super digestible manner.

Answer 1

Given:

The function is:

`4^((8-2x))=256`

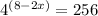
Find-:

The value of "x"

Explanation-:

The value of "x" is:

`4^((8-2x))=256`

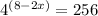
The 256 converts in 4 power then the value is:

`256=4^4`

So, the function becomes is:

`\begin{gathered} 4^((8-2x))=256 \\ \\ 4^((8-2x))=4^4 \end{gathered}`

If the base same then the power will also same for the function then,

`\begin{gathered} 4^((8-2x))=4^4 \\ \\ 8-2x=4 \end{gathered}`

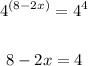
The value of "x" is:

`\begin{gathered} 8-2x=4 \\ \\ 8-4=2x \\ \\ 2x=4 \\ \\ x=(4)/(2) \\ \\ x=2 \end{gathered}`

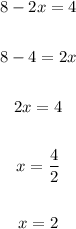
The value of "x" is 2.