Answer:
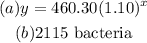
Step-by-step explanation:
Part A
An exponential regression is of the form:
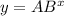
We plug this data into an exponential regression calculator:
To the nearest hundredth, the values obtained are:
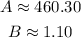
An exponential regression equation for this set of data is:
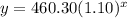
Part B
After 16 hours, when x=16
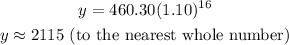
After 16 hours, the number of bacteria present is 2,115.