Question

Consider the following quadratic equation. -2x^2 - 4x = - 5STEP 1 of 2: Find the values of a, b, and c that should be used in the quadratic formula to determine the solution of the quadratic equation. a = -2 b = -4 c = 1STEP 2 of 2: Use the discriminate, b^2 - 4ac, to determine the number of solutions of the given quadratic equation. Then solve the quadratic equation using the formula X = (Formula to use is in the pic attached)

Answer 1

Given the equation:

`-2x^2-4x=-5`

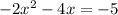
STEP 1 of 2:

To solve the equation using the formula

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

We need to find the values of a, b, and c.

To do that, the equation must be in the form:

`ax^2+bx+c=0`

Let's rearrange the terms of the given equation:

`-2x^2-4x+5=0`

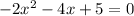
Now we can identify the values

a = -2, b = -4, c = 5

STEP 2 of 2: Calculate the value of the discriminant:

`\begin{gathered} d=b^2-4ac \\ d=(-4)^2-4\cdot(-2)\cdot5=16+40=56 \end{gathered}`

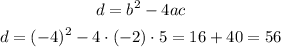
Since the discriminant is positive, the equation has two real solutions. Using the formula:

`x=\frac{-(-4)\pm\sqrt[]{56}}{2\cdot(-2)}=\frac{4+\sqrt[]{56}}{-4}=(4\pm7.483)/(-4)`

We have two solutions:

x = -2.87

x = 0.87

If we wanted to express the solutions in radical form, then we must simplify the expression:

`x=\frac{4+\sqrt[]{56}}{-4}`

Since 56 = 4 x 14 :

`\begin{gathered} x=\frac{4\pm\sqrt[]{4\cdot14}}{-4} \\ \text{Separating the roots:} \\ x=\frac{4\pm2\sqrt[]{14}}{-4} \\ \end{gathered}`

Dividing by -2:

`x=\frac{-2\pm\sqrt[]{14}}{2}`

Separating the solutions:

`\begin{gathered} x_1=\frac{-2+\sqrt[]{14}}{2} \\ x_2=\frac{-2-\sqrt[]{14}}{2} \end{gathered}`