ANSWER
Option 1
Step-by-step explanation
Parameters given:
Density of oil, ρo = 923kg/m^3
Density of water, ρw = 997 kg/m^3
Density of block, ρb = 966 kg/m^3
Height of block, h = 4.46 cm = 0.0446 m
To find the depth of the bottom of the block below the interface, since they are in equilibrium, we have to apply the equilibrium equation:
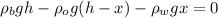
where x = distance of the bottom of the block below the interface
g = acceleration due to gravity
We have to solve for x by substituting the given values into the equation and simplifying:
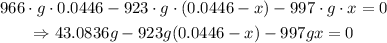
Dividing through by g:
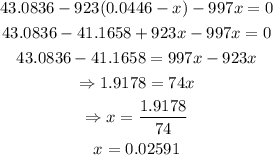
That is the distance.
The closest option is option 1.