Answer:
Removable discontinuity at x=0.
Explanation:
By looking at the denominator of h(x), there will be a discontinuity.
Since the denominator cannot be zero, x has to be different from 0. Therefore, there is a discontinuity at x=0.
Now, to determine what type of discontinuity, check if there is a common factor in the numerator and denominator of the function. If there is an existent common factor, there is a removable discontinuity or a hole.
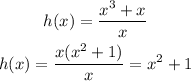
There is a removable discontinuity, or a hole, at x=0.