Question

Find algebraically the zeros for p(x) = x^3 + x^2 - 4x - 4. On the axes plot p(x)

Answer 1

`\begin{gathered} p\mleft(x\mright)=x^3+x^2-4x-4 \\ =\mleft(x^3+x^2\mright)+\mleft(-4x-4\mright) \end{gathered}`

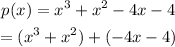
Now, let's factor this expression: taking x^2 out of (x^3+x^2) and -4 out of (-4x-4)

`=x^2(x+1)-4(x+1)`

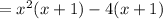
We have a common term, which is x+1, so we can factor the common term

`=\mleft(x+1\mright)\mleft(x^2-4\mright)`

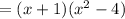
Now, we now that a^2-b^2 = (a-b)*(a+b) and we can apply that in x^2-4

`\begin{gathered} a^2-b^2=(a-b)\cdot(a+b) \\ x^2-4=(x-2)\cdot(x+2) \end{gathered}`

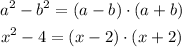
Therefore, our expression would be

`=\mleft(x+1\mright)\mleft(x+2\mright)\mleft(x-2\mright)`

Now, all we need to do to find the zeros of the expression is...

`\begin{gathered} x_1+1=0 \\ x_2+2=0 \\ x_3-2=0_{} \end{gathered}`

We need to solve for each value of x.

x1 = -1

x2 = -2

x3 = 2