Given:
Area of side surface of rectangular pyramid = 14.76 cm²
Total surface area = 18 cm²
Let's find the pyramid's altitude and the volume of the pyramid.
To find the altitude, H, let's first find the slant height.
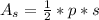
Where:
p is the perimeter of the base
s is the slant height
As is the area of the side surface.
• To find the perimeter of the base, let's find the base area.
Base area = Total surface area - Area of side surface.
Base area = 18 cm² - 14.76 cm² = 3.24 cm²
• Let's find the length of one side of the base:
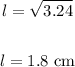
The length of one side of the base is 1.8 cm.
• To find the perimeter, apply the formula:
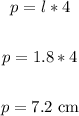
Let's plug in 7.2 cm for p, 14.76 for As and solve for the slant height s:
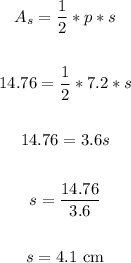
The slant height is 4.1 cm.
To find the altitude, H, apply Pythagorean theorem:
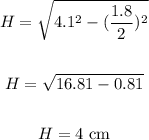
The pyramid's altitude, H = 4 cm.
To find the volume, apply the formula:
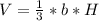
Where:
b is the base area = 1.8 x 1.8 = 3.24 cm²
H is the altitude = 4 cm
Thus, we have:
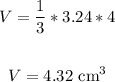
The volume is 4.32 cm³.
ANSWER:
• H = 4 cm
,
• V = 4.32 cm³