Question

Question 19 of 32A pendulum of mass 22 kg is released from rest at some height, as shown bypoint A in the image below. At the bottom of its arc at point B, it is traveling ata speed of 13 m/s. What is the approximate amount of energy that has beenlost due to friction and air resistance? (Recall that g = 9.8 m/s²)OA. 45 JOB. 134 JOC. 218 JOD. 297 J

Answer 1

Given:

The mass of the pendulum is,

`m=22\text{ kg}`

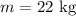
The height of release is,

`h=10\text{ m}`

The speed at point B is,

`v=13\text{ m/s}`

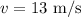
To find:

The approximate amount of energy that has been lost due to friction and air resistance

Step-by-step explanation:

The initial potential energy at point A, converts into kinetic energy at B.

The potential energy at A is,

`\begin{gathered} PE=mgh \\ =22*9.8*10 \\ =2156\text{ J} \end{gathered}`

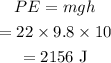
The kinetic energy at B is,

`\begin{gathered} KE=(1)/(2)mv^2 \\ =(1)/(2)*22*13^2 \\ =1859\text{ J} \end{gathered}`

The energy at B is not equal to the energy at A. So, there is a loss of energy due to the friction and air resistance and this loss is,

`\begin{gathered} 2156-1859 \\ =297\text{ J} \end{gathered}`

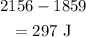
Hence, the loss of energy is 297 J.