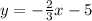Question

write a linear equation in slope intercept form with the given information.passes through (-6,-1) and is parallel to y=-2/3X +1

Answer 1

The general form of a linear equation in the slope-intercept form is:

`\begin{gathered} y=mx+b \\ \text{Where m is the slope and b is the y-intercept value} \end{gathered}`

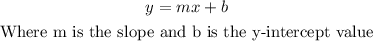
If the line we are looking for is parallel to y = -2/3 x + 1, so their slopes are the same, so m=-2/3 in the above equation.

And also we know that the line passing through the point (-6, -1), so:

`\begin{gathered} y=-(2)/(3)x+b \\ We\text{ evaluate the equation in the point (x,y)=(-6, -1) and find the value of b:} \\ -1=-(2)/(3)\cdot(-6)+b \\ -1=2\cdot(6)/(3)+b \\ -1=2\cdot2+b \\ -1=4+b\Rightarrow b=-1-4=-5 \end{gathered}`

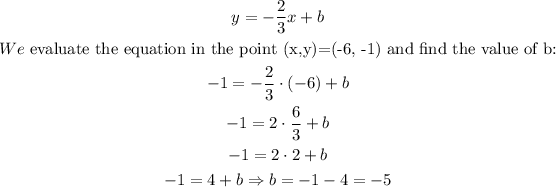
The equation of the line is:

`y=-(2)/(3)x-5`