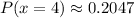Given that:
- The probability that an individual is left-handed is 12%.
- There are 30 students in the class.
You need to use this Binomial Distribution Formula, in order to find the probability of finding exactly 4 left-handed students :
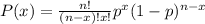
Where "n" is the number being sampled, "x" is the number of successes desired, and "p" is the probability of getting a success in one trial.
In this case:
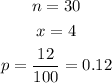
Therefore, by substituting values into the formula and evaluating, you get:

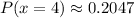
Hence, the answer is: