Question

Ms. Brooks put $1200 in a3retirement account that offers8% interest compounded annually.Ms. Brooks makes no additionaldeposits or withdrawals. How muchinterest will Ms. Brooks have earnedat the end of 2 years?

Answer 1

- We are required to find the compound interest on a $1200 invested in a retirement account if it is compounded annually at 8% interest for 2 years.

- In order to find the compounded interest, we use the formula:

`\begin{gathered} A-P=I \\ \text{where,} \\ A=\text{ Amount compounded after n years} \\ P=\text{ Principal or Initial Amount} \\ I=\text{ Compounded interest} \end{gathered}`

- But before we can use the above formula, we need to first calculate the Amount compounded. This can be gotten using the formula below:

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ \\ \text{where,} \\ n=\text{ The number of times the interest in compounded per year} \\ t=\text{ Number of years} \end{gathered}`

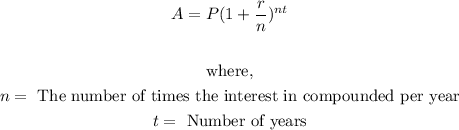
- Thus, we can proceed to solve the question by first finding the Amount compounded over the 2 years and then going on to calculate the compound interest.

Compounded Amount:

We can find the compounded amount as follows:

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ \\ A=1200(1+(8)/(100*1))^(2*1) \\ \\ A=1200(1+(8)/(100))^2 \\ \\ A=1399.68 \end{gathered}`

-

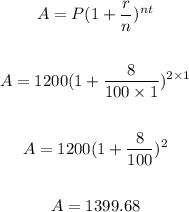
Compounded interest

`\begin{gathered} I=A-P \\ I=1399.68-1200 \\ \\ \therefore I=199.68 \end{gathered}`

Final Answer

The interest is $199.68