Question

On a test that has a normal distribution, a score of 54 falls two standard deviations

above the mean, and a score of 42 falls one standard deviation below the mean.
Determine the mean of this test.

Answer 1

Let μ be the mean of the distribution and let σ be its standard deviation.

We know that 54 falls two standard deviations above the mean, this can be express as:

`\mu+2\sigma=54`

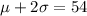
We also know that 42 falls one standard deviation below the mean, this can be express as:

`\mu-\sigma=42`

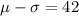
Hence, we have the system of equations:

`\begin{gathered} \mu+2\sigma=54 \\ \mu-\sigma=42 \end{gathered}`

To find the mean we solve the second equation for the standard deviation:

`\sigma=\mu-42`

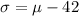
Now we plug this value in the first equation:

`\begin{gathered} \mu+2(\mu-42)=54 \\ \mu+2\mu-84=54 \\ 3\mu=138 \\ \mu=(138)/(3) \\ \mu=46 \end{gathered}`

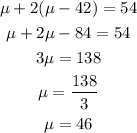
Therefore, the mean of the distribution is 46