Question

Part 1 of 3Points: 0 of 1For the function below, find (a) the critical numbers; (b) the open intervals where the function is increasing; and (c) the open intervals where it is decreasing.f(x)=2.8+1.6x-0.3x²(a) The critical number(s) is/are.(Type an integer or a simplified fraction. Use a comma to separate answers as needed.)

Answer 1

(a) The critical number is 8/3

(b) Increasing on (-∞, 8/3)

(c) Decreasing on (8/3, ∞)

Explanation

(a) Given the function:

`f(x)=2.8+1.6x-0.3x^2`

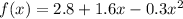
To find the critical number, first, we need to compute the derivative of f(x), as follows:

`\begin{gathered} (d)/(dx)f(x)=(d)/(dx)(2.8+1.6x-0.3x^2) \\ f^(\prime)(x)=(d)/(dx)2.8+(d)/(dx)1.6x-(d)/(dx)0.3x^2 \\ f^(\prime)(x)=0+1.6(d)/(dx)x-0.3(d)/(dx)x^2 \\ f^(\prime)(x)=1.6-0.3\cdot2x \\ f^(\prime)(x)=1.6-0.6x \end{gathered}`

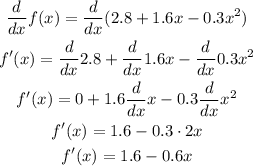
The critical numbers are those numbers where f'(x) is equal to zero. In this case:

`\begin{gathered} 0=1.6-0.6x \\ 0-1.6=1.6-0.6x-1.6 \\ -1.6=-0.6x \\ (-1.6)/(-0.6)=(-0.6x)/(-0.6) \\ (8)/(3)=x \end{gathered}`

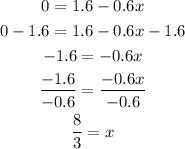
(b) Now, we need to evaluate f'(x) in the interval of values less than the critical number and the values greater than the critical number. Taking for example x = 2 (2 is less than 8/3), we get:

`\begin{gathered} f^(\prime)(x)=1.6-0.6x \\ f^(\prime)(2)=1.6-0.6\cdot2 \\ f^(\prime)(2)=0.4 \end{gathered}`

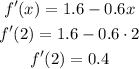
Given that f'(x) is positive, then f(x) is increasing in the interval (-∞, 8/3)

(c) Taking now for example x = 3 (3 is greater than 8/3), we get:

`\begin{gathered} f^(\prime)(x)=1.6-0.6x \\ f^(\prime)(3)=1.6-0.6\cdot3 \\ f^(\prime)(3)=-0.2 \end{gathered}`

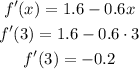
Given that f'(x) is negative, then f(x) is decreasing in the interval (8/3, ∞)