Question

Some the quadratic equation by completing the square.x^2+2x-5=0First choose the appropriate form and fill in the blanks with the correct numbers. Then solve the equation if there is more than one solution separate with commas.

Answer 1

Since the coefficient of the variable x is positive (+2), we will use the form:

`(x+a)^2=b_{}`

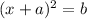
(That is, first option/form)

Then, to solve the equation by completing the square, since the coefficient of the variable x is 2, we need the number (2/2)^2 to show up, that is, number 1:

`\begin{gathered} x^2+2x-5=0 \\ x^2+2x+1-1-5=0 \\ (x+1)^2-1-5=0 \\ (x+1)^2-6=0^{} \\ (x+1)^2=6 \end{gathered}`

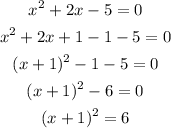
So the missing numbers in the first option are 1 and 6. Then, solving the equation, we have:

`\begin{gathered} (x+1)^2=6 \\ x+1=\pm\sqrt[]{6} \\ \begin{cases}x+1=\sqrt[]{6}\to x=\sqrt[]{6}-1 \\ x+1=-\sqrt[]{6}\to x=-\sqrt[]{6}-1\end{cases} \end{gathered}`

So the solutions are x = √6 - 1 , -√6 - 1