Question

Find the missing side lengths using trig ratios.61010у y29°BX ХVyaTo find the perimeter, you add all the side lengths. So, the perimeter of this triangle is

Answer 1

x=8.746, y=4.848 and 2P=23.594

1) Since we have the angles and the hypotenuse, we can find the missing legs by applying the following trigonometric ratios:

`\begin{gathered} y=\sin (B) \\ y=\frac{opposite\text{ leg}}{\text{hypotenuse}} \\ y=\text{ sin(}29) \\ (y)/(10)=\sin (29) \\ y=10\cdot\sin (29) \\ y\approx4.848 \end{gathered}`

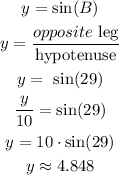
2) For the missing leg x, we can write out in terms of the cosine (29) or sine (61)

`\begin{gathered} \cos (29)=(x)/(10) \\ x=10\cdot\cos (29) \\ x\approx8.746 \end{gathered}`

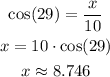
3) And finally, the Perimeter (2P) is equal to:

2P = 4.848 +8.746+10

2P=23.594

Rounding off to the nearest thousandth.